Q&A for Quantisweb Technology
This section consists of questions received about the Quantisweb Technology, and the responses given. The document regroups the questions in three distinct sections: Functional, Statistical and Optimization questions.
- The functional section regroups all questions that relate to the “what” the inputs, outputs, the process, and operational to the Quantisweb tool.
- The statistical section regroups all questions referencing to statistical issues, assumptions, and especially in the area of statistical models, variability, linearity and non-linearity, confidence interval, and design of experiments, etc.
- The optimization section regroups all questions pertinent to the optimizer, the algorithm, and optimality of solutions.
1. When interpreting some of the technical information in your website, are you saying that “Quantisweb” provides solutions with “Np+1” number of experiments; so if there are five (5) continuous inputs does this mean you recommend six (6) experiments?
Yes, if all variables inputs are continuous.
2. Is the “Np” the number of inputs which affect consequences?
Yes, these are the decision variables.
3. Are you stating that it is possible to input a mix number of levels or intervals for each of the parameters?
Yes, one can have as many levels as there are variables and the matrix can be uneven. E.g. 50 variables by 50 levels.
4. If I have 3 variables with 3 levels, are you stating that in the case of design of experiment for a complete full factorial design with 27 experiments, I need only 4 experimental trials to determine the optimal solution?
Yes. The statement is correct. In addition, one includes information on the desired end product by stating the ideal property values desired, and other information as listed in the answer to Question #8.
5. Will you confirm that your software will give me an optimal solution desired in four experiments for the following example? Example: in a chemical experiment where I want to produce methane to heat a building and my objective is to obtain a 90% or more methane. There are three variables: PH, temperature, and Time/Residence working with three levels. If the minimum temperature (15 C) and maximum (55 C) gives 10% of methane but the optimal is attained at a temperature of 40 C (Gaussian curve)?
Yes. You will get an optimal solution for the parameters and ranges used, as long as all other decision variables are kept constant, and there is no large variability detected. In the case, where large variability exists then you will get an optimal combination of values in a region of optimality and iterations may be necessary.
6. If in the methane example above, the intervals are reduced to two levels; can it be presumed that the system will not generate the optimal solution?
No, Quantisweb is not restricted by the concept of levels.
7. Can the system be used to reduce the number of simulation runs?
Yes. However, the minimum number of runs is Np + Nc +1. Where Nc is the number of nominal (classification) values.
8. What inputs must the user provide in order to run the optimization algorithm?
The user must input the following into Quantisweb:
- The properties of the product or process
- The ideal values of these properties
- A ratio of importance between each pair of properties in a comparison matrix for each level in the hierarchy, on a scale of 1 to 7.
- The Np parameters (continuous or discrete) and the range of values Nv levels for each parameters.
- Any constraint that exists representative of the experimental conditions amongst any of the parameters.
- The result of experiments (ROE) from the experiments performed according to the experimental values.
9. Can the user provide additional or alternative experimental values in order to run the optimization algorithm?
Yes.
10. What are the outputs of your algorithm to the end user?
- Relative and global weights for the ideal properties;
- Experimental values to be run;
- Behavioral laws;
- The existence of any large variability, if any;
- The optimal combination of values (OPV)
- The probability property value (PPV)
- Linear Relationship Table
11. Is the statistical model considered an output?
These models generated on a number of restricted tests Np + Nc +1, are behavioral laws. They are better utilized as indications of patterns and not robust enough to be considered statistical models.
12. Can you customize your approach to meet specific needs?
Yes, because the problem is defined by the user and his environment and his specific needs.
13. Can you complement simulation technologies?
Yes, instead of having product characteristics you have model characteristics. The deterministic simulation can be completed with random models generated from the Result of Experiment (ROE).
14. In addition to the data from the experiments, are any other source of information used?
No, if the user has provided all the input required, such as the ideal properties, performed the pair-wise, and provided the parameters (variables) and the necessary constraints, and the results of experiments, the system has all the information it requires to perform the optimization and generate an OPV for the Np + Nc +1, experiments.
15. What combination of continuous and discrete variables is allowed?
No limit.
16. How does it compare and does it replace any of the following: Minitab, Matlab, Monte Carlo Simulation, Statistica?
Quantisweb is a patented multi-objectives (targets) and multivariate Stochastic Approximation Optimization methodology that generates the behavioral laws of a problem and the Optimal Parameter Values of its solution, whereas the other tools are simulation software or statistical software.
17. How is the ratio of importance between two properties assigned?
Using the AHP approach developed by Thomas Saaty, it is done by comparing two properties at a time on a scale of 1 to 7, known as the pair-wise comparison.
18. What allows one to establish the ratio of importance in the pair-wise comparison?
The expertise and the experience of the user complemented by a consistency index provided by the system will one to establish the ratio of importance. This ratio of importance becomes incorporated in the objective function and used in optimization.
19. Must one use the pair-wise comparison or AHP method?
No, one can enter weights with values at random or leave weights to be equally distributed, that is, by default the ratio is 1 to 1, which in turn comes incorporated in the objective function and used in optimization.
Statistical
20. What hypotheses are made for this methodology?
For properties whose values are continuous, we assume that the experimental error is null or negligible or controllable. For example, in a case where we have two parameters, all experiments that include parameters with values X1 = 10 and X2 = 4 should obtain the same or a similar value for Y.
Furthermore, if the hypothesis stipulates that the experimental variability of each property is continuous in nature then repetition of the same experiments are not needed.
21. The statistical/behavioral model observed is linear with one bilinear term with respect to the free parameters per model output. Are there restrictions to the form of the statistical model?
No. The form of the statistical model generated can be multi-linear, quadratic, and/or consist of more degrees of freedom for properties that are continuous in nature. The statistical model will be of type “logistic” in form for those properties that are binary. Thus, there aren’t any restrictions to the form of the statistical model, apart from the fact that the statistical models are based upon a minimum number of tests, Np + Nc +1.
22. Can the end user change the structural form of this model for a particular problem?
No, the system chooses the model for the problem.
23. Do you provide statistical measures for the degree of uncertainty or confidence intervals for the optimal solution/optimal parameter values?
No, statistical measures for the degree of uncertainty or confidence intervals is not provided as such. The statistical estimation is based on a restricted number of tests, Np + Nc +1, therefore cannot be used to define confidence intervals.
Quantisweb does not perform statistical analysis found in statistical software, however it will provide a probable property value (PPV) based on the trend of behavioral laws. Quantisweb is a global methodology, whose sole objective is to reach the optimal region (area) of the desired product.
24. Could data from a 1-dimensional or 2-dimensional sensitivity analysis (SA) i.e., varying parameters and assessing changes in system outputs, be used to improve your algorithm?
Our algorithm is optimal in achieving its purpose. In reference to number 20 above, there is no need to do a sensitivity analysis.
25. If a SA could provide valuable information, could the algorithm identify (perhaps a priori) which combinations of parameter variations would be required?
No.
26. How can we replace, or apply it in the context of sensitivity analysis?
It lends itself well in doing sensitivity analysis. The sensitivity of decision variables on design objectives is established through generated behavioral laws in the model. Refer to point number 24.
27. If one of the variable’s variability has a nonlinear influence on the response surface, will the software give an optimal solution based on the desired objectives?
Yes, it will.
28. Given a large variability, can we assume that the solution generated by the software cannot be the best solution possible?
In the case, where large variability exists then you will get an optimal combination of values in a region of optimality. In this case, the user can rerun the test by narrowing the ranges of intervals based on the OPV generated and narrow the region of optimality to reach the desired properties defined initially.
29. Are you claiming that your application can deal with non-linearities, such as consequences being a non-linear relationship of the inputs?
Yes.
30. Regardless of the number of levels for each of the inputs, how can this be sufficient to create a linear model for a consequence and also to understand the level of noise that exists; much less non-linearities?
It is sufficient because of the innovation developed by the integration of three mathematical domains: decision theory, statistics, and optimization which translates by:
- The way the application estimates the interaction of the X’s using a combination of parametric and/or nonparametric methods to generate Np + Nc +1 experimental values.
- The way the application uses the Y’s measured from these experimental values to sequentially generate the behavioral laws based on the descending order of the importance of the Y’s.
- The way the application generates a goal function that generalizes the loss function of Taguchi in multidimensional.
31. Please explain how you create non-linear predictive models (equations) which fit the true response (not just the data) better than what statistics can do with six experiments (when there are five inputs to be defined)?
We do not create non-linear predictive models which fit the true response; instead we create behavioral patterns, which are estimations for each of the response function.
32. Given the input/output data of the Np + Nc +1 experiments; what mathematical mechanism do you use to determine the optimal values of the vector x those results in y being closest to targets?
The application estimates the interaction of the X’s using a combination of parametric and/or nonparametric methods to generate Np + Nc +1 experimental values, then the application uses the Y’s measured from these experimental values to sequentially generate the behavioral laws based on the descending order of the importance of the Y’s, and finally the application generates a goal function that generalizes the loss function of Taguchi in a multidimensional case.
33. Please explain what “behavioral laws” represent and how you use them?
These behavioral laws are stochastic equations, representing estimations therefore called patterns and are not considered robust. They represent the behavioral patterns of each of the variables (x) for each of the properties (Y). Since the relationships of the variables (x) are processed simultaneously for each property (Y), the patterns generated are expressed in linear, quadratic, logistic equations.
They become part of the model to optimize.
34. I did notice that you do create linear prediction models, are they used for optimization?
If you mean the behavioral laws, yes they are used for optimization. Due to lack of robustness, these cannot be considered prediction models.
35. How about validity and representativeness of non-linear relationships with such small number of experiments?
These behavioral laws are estimates and only produce a global perspective of the observed phenomenon whether the problem is linear or non-linear. These models based on a reduced number of experiments Np + Nc +1 should not be regarded as a final achievement on its own, but a transitional stage in the optimization process. The optimization process objective is to produce either optimal values of the parameter X, in case all characteristics are regular; or a simultaneous optimality of all characteristics in cases where at least one characteristic has a large variability. The objective is not to understand the process.
36. If it is non-linear, what are the assumptions?
We assume that we have: Np parameters (ingredients), X1, ….XNp. that may be continuous or discrete. Y1…YK properties (goal function) that may be continuous or binary. Each parameter accepts Nv levels (values).
For properties whose values are continuous, we assume that the experimental error is null or negligible or controllable. For example, in a case where we have two parameters, all experiments that include parameters with values X1 = 10 and X2 = 4 should obtain the same or a similar value for Y.
Furthermore, if the hypothesis stipulates that the experimental variability of each property is continuous in nature then repetition of the same experiments are not needed.
To assure the convergence of the optimization, the number of continuous parameters cannot be greater than the number of discrete parameters. If the number of parameters is small (inferior to 8), generally the interactions among the parameters are negligible in the model (patterns).
37. What types of mathematical equations are provided?
Equations can be Linear, Quadratic, and Cubic, or logistic.
38. What can we extract from the behavioral laws?
The behavioral laws will provide the patterns or pattern from the behavior of each parameter in respect to the property. Furthermore, it can assist in extracting the critical and non-critical variables for that given problem, relationships, and probability values.
39.How robust are these patterns?
In most of the Np + Nc +1 context, the behavioral patterns are estimations and cannot be considered robust.
40. Can these patterns be rendered robust? If yes, how?
Yes, the robustness can be increased by increasing the number of experiments to a level respecting the statistical laws.
41. How should we deal with variability?
In the case, where large variability exists then you will get an optimal combination of values in a region of optimality.
42. Is variability dealt with when the number of experiments increases?
No.
43. Is variability reduced or eliminated when the OPV is brought back as an input to the system and re-optimized?
Variability cannot be reduced nor eliminated, however the user can rerun the optimization by including the OPV generated as a solution to reduce the region of optimality rendering the solution more robust.
44. Does it do screening?
Yes, Quantisweb can be used to do screening.
45. Is the DOE done using orthogonality design, collinearity, correlability, rotability?
No.
46. Does it do a grid search?
No.
47. Is it a probabilistic design?
No.
48. Is it similar to Minitab (rule next highest power?)
No.
49. Are the selected directions (i.e., experimental design) optimal or optimized?
No.
50. What is the theoretical mathematical proof of optimality?
The theoretical proof of optimality can be found in a white paper. The first three applications sited in the white paper address most of the traditional DOE methods used in formulation. The comparison of the results from the classical approach with the Quantisweb minimal mDDOE based on Np +Nc + 1 proves that optimality attained is more precise than those attained from the classical approach.
51. How does your algorithm scale with increasing Nv?
It is not dependent on Nv like the classic DOE where it has an exponential effect. Our algorithm depends on Np, number of parameters only, and the effect is additive only.
52. What kind of factor analysis is used?
Our system does not make statistical inferences; statistical inferences or factor analysis is performed in the objective to understand the phenomenon. The objective of our system is not to understand the process but to produce either the optimal values of the parameters (X), in case all characteristics are regular; or a optimality region of all characteristics, in the case of at least one characteristic has a large variability.
Optimization
53. What optimization approach are you using?
The optimization is done using the largest possible library with or without constraints. The types of constraints used automatically direct the system toward the most adapted method to the case of concern. For example if the following constraints are declared:
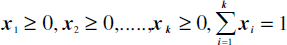
then the system will be aware that it is dealing with a mixture problem and hence it will apply either the Simplex or improved Simplex method according to the number of discrete variables involved.
A complete collection of mathematical and statistical algorithms for high performance computing applications. IMSL (Integrated Mathematics Statistics Library) is used.
54. Is the optimization algorithm iterative?
Yes.
55. How “smooth” must the response surface be?
This question does not apply to Quantisweb because the response surface method is not used by the Quantisweb methodology.
56. How can one judge if the response surface is “smooth enough” for an accurate solution?
Given that we do not utilize RSM, the term “smooth enough” can only be translated and interpreted in the context of Quantisweb. For the purpose of discussion, we will adopt the term “smooth’ in the Quantisweb methodology. Quantisweb detects the properties with large variability for quality control, based on both the parametric and non-parametric methods.
If the system does not detect any large variability from any of the properties, then it implies that we are facing a problem consisting of “smooth” properties only.
In this case, the solution generated by the system is global optimal because it satisfies all the properties simultaneously, thus giving a unique optimal solution.
57. Can you use your algorithm to identify local optima or are you constrained to identifying only the global maximum?
Quantisweb generates the local optima which is the global optima. The definition of the “local” in Quantisweb is limited by the interval imposed upon the various parameters and the imposed constraints. In the case where at least one of the properties is detected to have large variability, the optimal solution generated will be in the zone of global optimality which of course lies within the imposed interval limits.
58. Is this an optimization tool to do fine tuning?
It can be used to do fine tuning among the many tasks of research and development, as well, as in a production environment.
59. Is it very important to know the minimum and maximum of the variables so that we don’t end up with the wrong zone, and therefore wrong results?
No. The tool will find the exact parameter value within the intervals stipulated by the scientist/engineer. However, if the interval is erroneous, the tool will warn the user that the response may lie outside that interval. At this point the user has the option to modify the intervals and regenerate a new set of experimental values.
60. For those who want to understand the limitations of the software, can you explain in more depth the details of the methodology that determines the optimization?
The patented integration of the three domains of mathematics: decision theory, statistics, and optimization govern and define the innovation. The integration leads to the global approach which results in the possibility to deal with complex multivariate problems, and multidimensional problems. The power of the application is best realized with complexity.
61. Do you deal with convex and non-convex problems?
Yes, we deal with both.
62. How does it deal with “convex” problems?
The goal function is convex, and the multivariate convex function is optimal, unique if the problem shows no variability.
63. How does it deal with “quasi convex” problems?
If the problem shows at least one property “Y” with large variability, the goal function is non-convex, the application will select a quasi-convex optimization method, and the answer will be in a zone of optimality.
64. Is the optimizer a deterministic or a stochastic optimizer?
It is a deterministic optimizer utilizing random models based on the result of experiment (ROE).
65. Is the application deterministic or non-deterministic?
Non-deterministic.
66. If you have a “dynamic Y”, can we attain the minimum function?
This does not apply in Quantisweb technology.
67. Does the system handle both deterministic and stochastic problems?
Yes. The system deals with both stochastic and deterministic problems. However, it will generate the model (the behavioral laws) of a stochastic problem only, since the deterministic laws are already known.
68. How does the system handle false minima?
The False Minima (Local Minima) is handled by the optimizer, by exploring multiple points of the design space, such as, but not limited to, restarting an optimization from each minima until the best minima is reached.
However this process does not guarantee to find the global minima in a non-linear problem that manifests a large variability. In situations such as these, the application will propose a certain number of solutions to be validated. When and if validated, the information generated will be used to minimize once more the zone of optimality.
